Notes on the Membrane

Multimodality has led to some tweaks to the standard Transformer recipe. In this post we will cover QK Normalization (QKNorm), where we apply normalization to the query and key vectors in the attention mechanism. This has become an important step for unified input models where we have tokenized representations of text, images and other modalities present in a single sequence. These types of models are very prone to training instability without appropriate normalization, as the norms of the Q and K vectors can grow dramatically during training. QKNorm is an effective stabilisation technique for this problem, and has been important in several large-scale vision and multimodal recipes, although it is not the only option and not always sufficient on its own.

One note on terminology before we start. The original method of Henry et al (2020) L2-normalizes the queries and keys and introduces a learned scaling parameter. What most of the recipes below use, and what we implement at the end of this post, is RMSNorm or LayerNorm applied to q and k while keeping the usual \(1/\sqrt{d_h}\) scaling. That is a reasonable variant, but it is not quite the original method.

Attention logits are constructed via a scaled dot product in the Transformer attention mechanism. Writing the logits as \(\mathbf{S}\) and the attention weights as \(\mathbf{A}\):

\[ \mathbf{S} = \frac{\mathbf{Q} \mathbf{K}^\top}{\sqrt{d_h}}, \qquad \mathbf{A} = \text{softmax}(\mathbf{S}) \]

The softmax is invariant to translation. If we add a constant \(c\) to each element of the input vector \(\mathbf{s}\) then we can see that:

\[ \text{softmax}(\mathbf{s} + c) = \frac{e^{\mathbf{s} + c}}{\sum_j e^{s_j + c}} = \frac{e^c \cdot e^{\mathbf{s}}}{e^c \cdot \sum_j e^{s_j}} = \frac{e^{\mathbf{s}}}{\sum_j e^{s_j}} = \text{softmax}(\mathbf{s}) \]

The invariance property is a potential source of training instability when combined with unnormalized query and key vectors.

To see why, we can write an individual logit of the attention matrix as:

\[ \text{s}_{ij} = \frac{\|\mathbf{q_i}\| \|\mathbf{k_j}\| \cos(\theta_{ij})}{\sqrt{d_h}} \]

Since additions have no impact on the relative magnitudes of the logits, the only way for the model to increase the relative distance between logits is by increasing or decreasing the norms of the \(\mathbf{q}\) and \(\mathbf{k}\) vectors, or adjusting the angle \(\cos\left(\theta_{ij}\right)\). It may be easier for the model to learn to increase the norms, as this requires uniform scaling of weights, as opposed to changing the angles which requires coordinated changes in multiple weight parameters.

However, uncontrolled growth in the norms of these vectors can lead to instabilities in training, as large gaps between logits will collapse attention weights to one-hot vectors - "attention entropy collapse" (Dehghani et al 2023, Zhai et al 2023).

It is worth being careful about what is doing the work here. The softmax has no special threshold of absolute logit magnitude beyond which it misbehaves. Its Jacobian is \(\partial p_i / \partial s_j = p_i(\delta_{ij} - p_j)\), whose entries are bounded. And in exact arithmetic \(\text{softmax}([50000, 50001])\) is identical to \(\text{softmax}([0, 1]) \approx [0.269, 0.731]\), which is nowhere near one-hot. What matters is the gap between the winning logit and its competitors, not the absolute size of the logits. So growing query and key scales are a problem because they stretch those gaps, driving attention towards highly concentrated distributions, and not because the logits enter some exponential region of the softmax.

Recent empirical evidence suggests that introducing multimodal inputs increases hyperparameter instability, and makes training more prone to norm explosion. We cover the relevant literature in the next section.

Dehghani et al (2023) observed divergent training with an 8B Vision Transformer. The loss decreased as normal to begin with, but within 2,000 steps it steadily increased. Without normalization they found that attention logits grew to over 50,000 in magnitude, resulting in one-hot attention weights post-softmax and subsequently unstable losses and gradients:

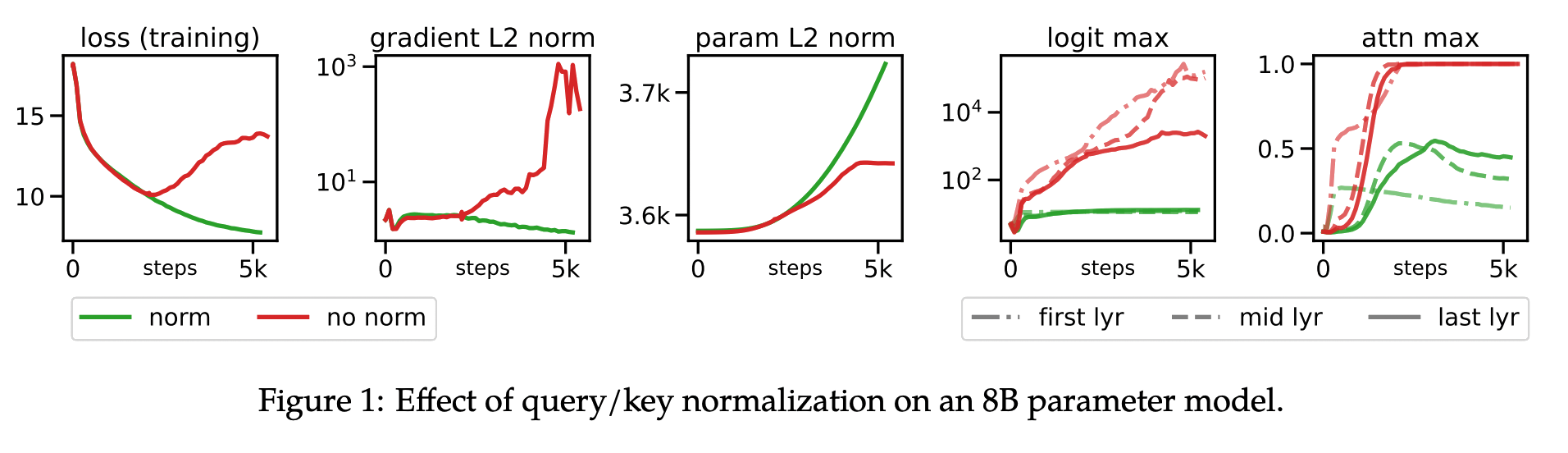
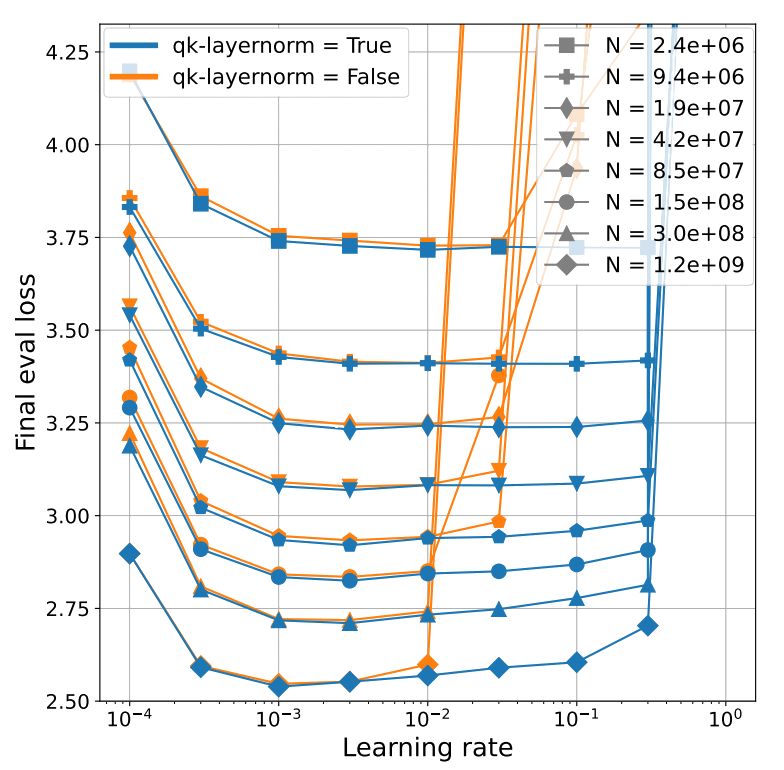
Wortsman et al (2023) found they could obtain attention logit instability with smaller models using higher learning rates. As a solution, they found that QKNorm together with z-loss regularization enabled stable training across three orders of magnitude of learning rate (LR) variation.

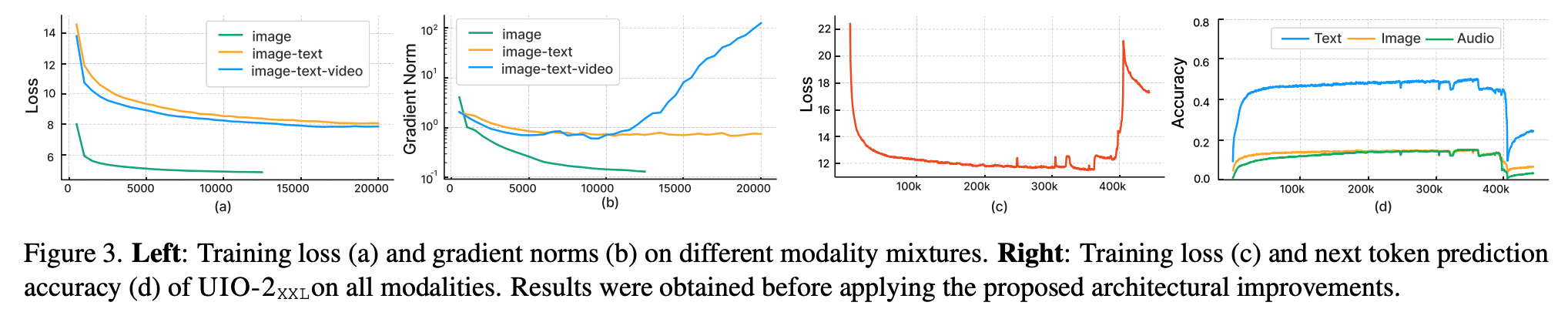
Two caveats on that result. Their setup is text-only C4, so it is not in itself evidence for a multimodal mechanism. And they report that the logit growth instability "is not due to the softmax in the self-attention layer, as it still occurs with a pointwise variant of attention". Any explanation that makes softmax competition the necessary cause of norm growth has to account for that.

Lu et al (2023) experienced unstable training as they integrated additional modalities into their UnifiedIO architecture. They observed extremely large values in the multi-head attention logits when including image and audio modalities, leading to one-hot attention weights. They used QKNorm to stabilise training, although it is part of their fix rather than all of it. They found that "even with QK normalization, the attention logits in the perceiver can grow to extreme values", so they also apply scaled cosine attention in the perceiver resampler and compute attention logits in float32.

Chameleon Team (2024) experienced instabilities in the mid-to-late stages of training which they attributed to uncontrolled norm growth. They attribute norm growth to "norm competition" between modalities of differing entropy, which is encouraged by softmax translation invariance. They note this becomes problematic once the logits grow beyond what bfloat16 can resolve. It is worth being precise that this is a precision problem rather than an overflow one: bfloat16 reaches up to around 3e38, but 50000 and 50001 both round to 49920, so the gap between two competing logits can be destroyed before the softmax ever sees it. They do not observe the same problem for the unimodal text-only setting.

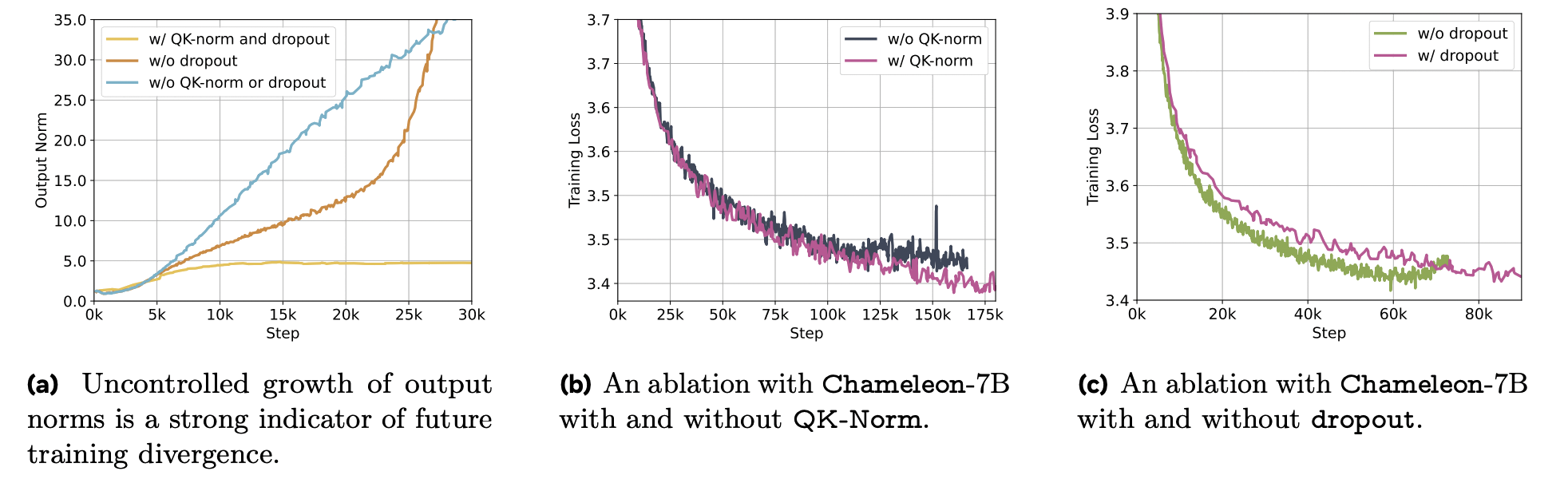
Interestingly, they found that QKNorm alone was not sufficient for stabilising training with the LLaMA architecture. They opt for a Swin Transformer normalization strategy, which normalizes the outputs of the attention and feedforward branches before they are added back to the residual stream. This is not the same as conventional post-LayerNorm, which normalizes after the residual addition.

Some other recent work includes OLMoE by Muennighoff et al (2024), where they find QKNorm increases training stability, at a cost of around 10% throughput in their implementation. Additionally Ramapuram et al (2024) find QKNorm significantly stabilises performance by making Sigmoid Attention and Softmax Attention less sensitive to learning rate changes. That result is for their language modelling experiments; in vision they find Sigmoid Attention is robust with or without QKNorm.

This is the most speculative part of the post, so it is worth separating what is established from what is conjecture.

Let's look at the \(\mathbf{q}\) and \(\mathbf{k}\) vectors again. For a single head, the query is constructed via a linear layer (omitting biases):

\[ \mathbf{q} = \mathbf{x} \mathbf{W_{q}} \]

where \(\mathbf{x}\) is of size \(\left(T,C\right)\) and \(\mathbf{W_q}\) is of size \(\left(C, d_h\right)\). One thing to note is that \(\mathbf{x}\) here is the input to the projection, which in a pre-norm Transformer is a normalized hidden state rather than the raw token embedding. That matters for any explanation appealing to raw embedding scale, since RMSNorm removes the radial scale of whatever goes into it.

Holding the weights fixed, and letting the row vector \(\mathbf{x_t}\) have mean \(\mathbf{\mu}\) and covariance \(\mathbf{\Sigma}\), the expected squared norm of a query is:

\[ E[\|\mathbf{q_t}\|^2] = \text{tr}\left(\mathbf{W_q}^\top \mathbf{\Sigma} \mathbf{W_q}\right) + \|\mathbf{\mu} \mathbf{W_q}\|^2 \]

which follows from expanding \(\|\mathbf{x} \mathbf{W_q}\|^2 = \mathbf{x} \mathbf{W_q} \mathbf{W_q}^\top \mathbf{x}^\top\) and taking expectations. The simpler expression:

\[ E[\|\mathbf{q_t}\|^2] = \sigma_{x}^2 \cdot \|\mathbf{W_q}\|^2_{F} \]

is the special case where the activations are zero-mean and isotropic, i.e. \(\mathbf{\mu} = 0\) and \(\mathbf{\Sigma} = \sigma_{x}^2 \mathbf{I}\). Unimodal inputs do not guarantee that, and the quantity is not constant during training either, since both the weights and the activation distribution are moving.

The multimodal version conditions on the modality \(m\):

\[ E[\|\mathbf{q_t}\|^2 \mid m] = \text{tr}\left(\mathbf{W_q}^\top \mathbf{\Sigma}_m \mathbf{W_q}\right) + \|\mathbf{\mu}_m \mathbf{W_q}\|^2 \]

So different modalities can certainly have different expected query norms. What this does not tell us is which modality has the larger norms, or that any gap between them compounds.

A tempting argument here is that images have less structure than text and are more variable (higher entropy), so image tokens would have higher variance, larger query norms, and would therefore dominate attention. I do not think that argument works, for two reasons.

The first is that entropy and embedding scale are different quantities. Multiply every learned image embedding by 100 and the token distribution is unchanged, so its entropy is unchanged, while the embedding variance goes up by a factor of 10,000. Equally, a high-entropy token set can be given unit-norm embeddings. Higher token entropy therefore does not imply higher activation variance, and activation variance is what the expression above actually depends on.

The second is that a large query norm does not make a token receive more attention. Queries control how a token attends to others. Keys control how it is scored as a target. Scaling a query \(\mathbf{q_i}\) by a positive constant \(a\) changes that token's own attention row:

\[ p_{ij}(a) = \frac{e^{a s_{ij}}}{\sum_\ell e^{a s_{i\ell}}} \]

This sharpens or flattens how token \(i\) spreads its attention over the sequence. It does nothing to make other tokens attend to token \(i\), which is a property of its key. And even a large key norm is not sufficient, since the dot product depends on alignment: a large key orthogonal to a query still scores zero.

That leaves the competitive growth story as a hypothesis rather than something derived. It is Chameleon's proposed explanation for what they observed, and it is a plausible one, but the Wortsman result above, where logit growth persists with a pointwise attention variant, is evidence against softmax competition being the necessary mechanism.

What I think can be said is weaker. Different modalities induce different activation distributions and different optimisation pressures, and those can produce unequal query and key scales. Why that becomes self-reinforcing in some mixed-modal runs and not in text-only ones still looks like an open question.

For practical purposes, a simple fix is to normalize the query and key vectors before the attention mechanism. A reference PyTorch implementation is provided below.

import torch
import torch.nn as nn
import torch.nn.functional as F

class SelfAttention(nn.Module):
    def __init__(self, dim_size, n_heads, norm=nn.RMSNorm, use_qk_norm=False):
        super(SelfAttention, self).__init__()

        assert dim_size % n_heads == 0, "dim_size must be divisible by n_heads"

        self.dim_size = dim_size
        self.n_heads = n_heads
        self.head_dim = dim_size // n_heads

        self.qkv_attn = nn.Linear(dim_size, dim_size * 3, bias=False)
        self.project = nn.Linear(dim_size, dim_size, bias=False)
    
        self.use_qk_norm = use_qk_norm

        if self.use_qk_norm:
            self.q_norm = norm(self.head_dim)
            self.k_norm = norm(self.head_dim)

    def forward(self, x: torch.Tensor):
        B, T, C = x.size()

        qkv = self.qkv_attn(x)
        q, k, v = qkv.split(self.dim_size, dim=2)

        q = q.view(B, T, self.n_heads, self.head_dim)
        k = k.view(B, T, self.n_heads, self.head_dim)

        if self.use_qk_norm:
            q = self.q_norm(q)
            k = self.k_norm(k)

        q = q.transpose(1, 2)
        k = k.transpose(1, 2)
        v = v.view(B, T, self.n_heads, self.head_dim).transpose(1, 2)

        y = F.scaled_dot_product_attention(q, k, v, is_causal=True)
        y = y.transpose(1, 2).contiguous().view(B, T, C)
        y = self.project(y)
        
        return y

Note the transposes on q and k before the attention call. An earlier version of this post normalized them in \(\left(B, T, H, d_h\right)\) layout and passed them straight to scaled_dot_product_attention, which expects \(\left(B, H, T, d_h\right)\). That raises a shape error in the general case, and quietly computes the wrong thing in the special case where the sequence length happens to equal the number of heads.

It is also worth being precise about what the normalization buys you. With RMS normalization and no learned gains we have \(\|\mathbf{\hat{q}}\| = \sqrt{d_h}\), so Cauchy-Schwarz bounds each logit by \(\sqrt{d_h}\). But RMSNorm as normally implemented includes learned per-coordinate gains, and those gains can themselves grow during training, so the bound is not fixed and training-independent. What the normalization reliably removes is the dependence on the raw scale of the incoming vector. It does not make every source of logit growth impossible, which is consistent with Unified-IO 2 seeing extreme perceiver logits despite using QKNorm.

Thanks to Marcin Kardas and Michiel de Jong for proofreading this post.

Thanks to @assesseth for noticing a mistake with the mathematical derivation for the norms.

If you find my writing interesting, you can follow me at @rosstaylor90 on X.

QK Norm and the Curious Case of Logit Drift

What's the problem?

What's the evidence?

Why does multimodality lead to norm growth?

Implementation

Thanks

References