Notes on the Membrane

9 December 2024

The outer membrane of a neuron is a lipid bilayer approximately 7-10nm thick, separating the cell's interior from extracellular liquid. The concentration of ions differs within and outside the neuron, which creates a concentration gradient across the membrane. The typical ion concentrations for a mammalian neuron (Izhikevich et al., 2004, Delpire et al, 2014, Doyon et al, 2016) are:

Sodium: \([Na^+]_{out} = 145 mM\), \([Na^+]_{in} = 5-15 mM\)
Potassium: \([K^+]_{out} = 5 mM\), \([K^+]_{in} = 140 mM\)
Chloride: \([Cl^-]_{out} = 110-130 mM\), \([Cl^-]_{in} = 3-15 mM\)

The concentration gradient is maintained by the selective permeability of the membrane to different ions.

The high intracellular concentration of potassium (opposite for sodium) is maintained via a sodium-potassium pump, where an ATPase enzyme exports three sodium ions and imports two potassium ions (Delpire et al, 2014). This acts in the opposite direction of the concentration gradient.

Chloride ions are maintained at a low intracellular level through a \(K^+-Cl^-\) cotransporter known as KCC2, which is a protein embedded in the membrane (Ben-Ari et al, 2012). KCC2 moves \(Cl^{−}\) against its gradient by "piggybacking" on \(K^{+}\) as it moves down the \(K^{+}\) electrochemical gradient and out of the neuron.

The unequal distribution of ions creates an electrical potential across the membrane. At thermal equilibrium, the potential for a specific ion is described by a Nernst potential:

\[ E = \frac{RT}{zF} \ln{\left(\frac{[ion]_{out}}{[ion]_{in}}\right)} \]

where \(R\) is the gas constant, \(T\) is the temperature, \(z\) is the ion's charge, \(F\) is the Faraday constant, and \([ion]_out\) and \([ion]_in\) are the concentrations of the ion outside and inside the cell.

We can use this information to calculate the Nernst potential for sodium and potassium:

python

import numpy as np

# Concentrations (mM)
Na_out = 145
Na_in = 15 # we'll use upper end of concentration (commonly used)
K_out = 5
K_in = 140
Cl_out = 120
Cl_in = 9

# Constants
R = 8.314472  # Gas constant in J/(mol·K)
T = 310.15  # Temperature in Kelvin (37°C) - body temperature
F = 96485  # Faraday constant in C/mol
Z = 1  # Valence; e.g. 1 for a monovalent ion such as K+

def nernst_potential(ion_out, ion_in):
    return (R * T) / (Z * F) * np.log(ion_out / ion_in)

E_Na = nernst_potential(Na_out, Na_in)
E_Na_mV = E_Na * 1000  # Convert from volts to millivolts
print(f"Nernst potential for Sodium (Na⁺): {E_Na_mV:.2f} mV")

E_K = nernst_potential(K_out, K_in)
E_K_mV = E_K * 1000  # Convert from volts to millivolts
print(f"Nernst potential for Potassium (K⁺): {E_K_mV:.2f} mV")

E_Cl = nernst_potential(Cl_out, Cl_in)
E_Cl_mV = E_Cl * 1000  # Convert from volts to millivolts
print(f"Nernst potential for Chloride (Cl⁻): {E_Cl_mV:.2f} mV")

Nernst potential for Sodium (Na⁺): 60.63 mV
Nernst potential for Potassium (K⁺): -89.06 mV
Nernst potential for Chloride (Cl⁻): 69.23 mV

So the difference in concentration creates a Nernst potential of \(E_{Na} \approx +60mV\), \(E_{K} \approx -90mV\) and \(E_{Cl} \approx +70mV\).

To derive the resting membrane potential for all ions, we need to consider the permeability of each ion. Permeability is the capability of ions to flow across the membrane (whether they are moving or not). In contrast, conductance refers to the actual movement of charge across the membrane. The membrane is semipermeable as ion channels can be open or closed.

The resting membrane potential \(E_m\) is given by the Goldman equation, which takes into account all of the ions which are permeant through the membrane:

\[ E_m = \frac{RT}{F} \ln{\left(\frac{P_{K}[K^+]_{out} + P_{Na}[Na^+]_{out} + P_{Cl}[Cl^-]_{out}}{P_{K}[K^+]_{in} + P_{Na}[Na^+]_{in} + P_{Cl}[Cl^-]_{in}}\right)} \]

At rest, the neuron is a state of dynamic equilibrum with ionic currents flowing across the membrane but balancing out (Koch, 1999). The membrane in this state is more permeable to potassium ions as more channels are open. In a normal cell, the \(Na^+\) permeability is about 5% of \(K^+\) permeability or less (Chrysafides et al, 2023).

We can information on ionic permeability to calculate the resting membrane potential:

python

import numpy as np

# Concentrations (mM)
Na_out = 145.0
Na_in = 15.0 
K_out = 5.0  
K_in = 140.0 
Cl_out = 120.0
Cl_in = 9.0  

# Relative permeabilities (Pion)
P_K = 1.0   
P_Na = 0.04 
P_Cl = 0.4  # Example value; would need confirmation

# Constants
R = 8.314472    # Gas constant in J/(mol·K)
T = 310.15      # Temperature in Kelvin (37°C)
F = 96485.0     # Faraday's constant in C/mol

RT_over_F = (R * T) / F # volts

# Goldman equation
# For Cl- the concentrations are inverted due to its negative charge
numerator = (P_K * K_out) + (P_Na * Na_out) + (P_Cl * Cl_in)
denominator = (P_K * K_in) + (P_Na * Na_in) + (P_Cl * Cl_out)

Em = RT_over_F * np.log(numerator / denominator)
Em_mV = Em * 1000

print(f"Resting membrane potential (Em): {Em_mV:.2f} mV")

Resting membrane potential (Em): -68.75 mV

So the resting membrane potential is around \(−69mV\), meaning the neuron is negatively charged relative to the outside.

The lipid bilayer is a nearly perfect electrical insulator; it can sustain voltages in excess of \(\pm{150mV}\) (UPenn Bio251, 2003). Since it separates intracellular and extracellular ionic (conducting) fluids, it is functionally equivalent to a capacitor. A capacitor stores electrical energy by accumulating charge on two conductors separated by an non-conductive region, which can be a vacuum or an electrical insulator such as the lipid bilayer.

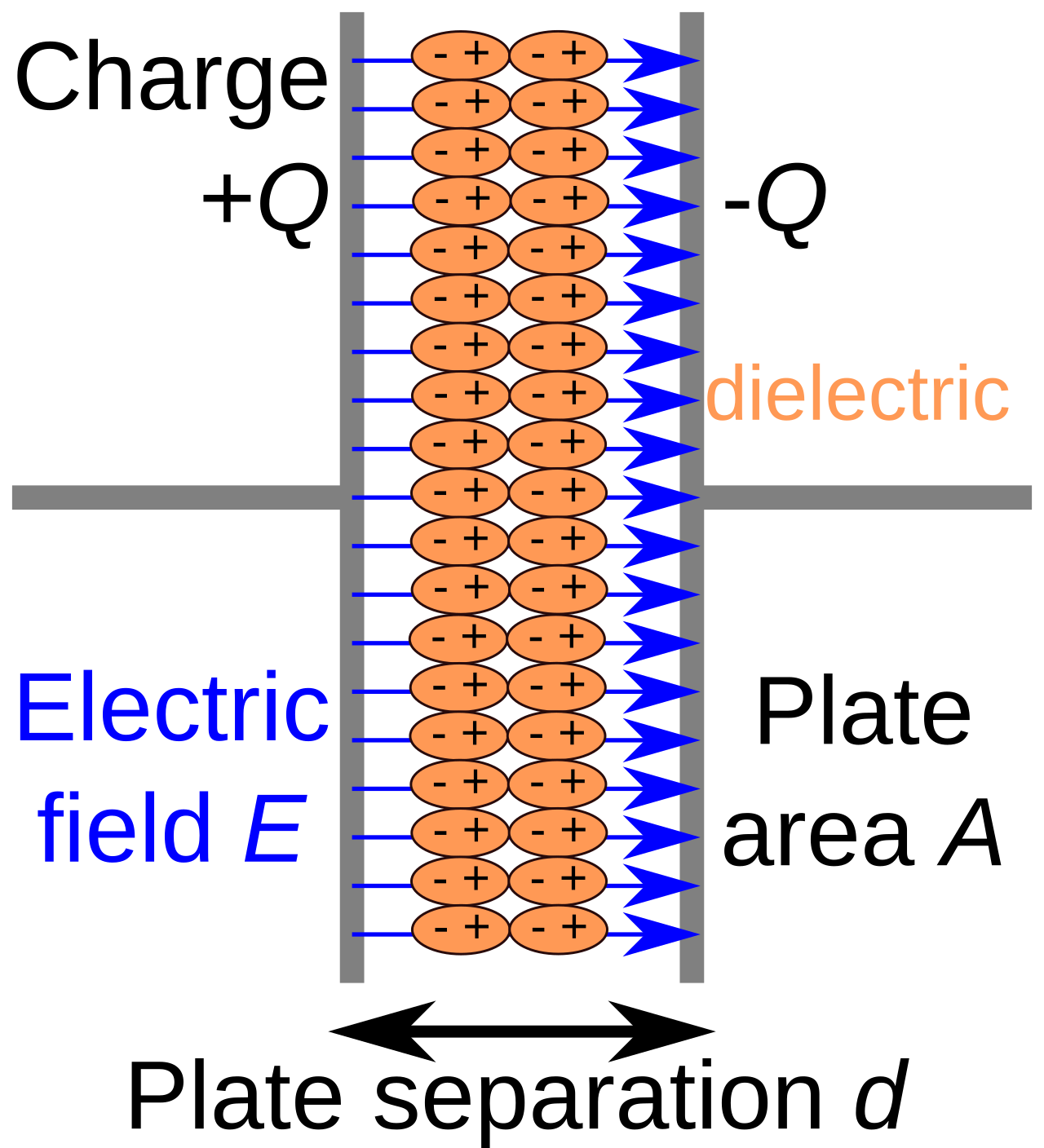
A charge on one conductor will induce a charge of equal magnitude but opposite sign on the other conductor, which means the dielectric develops an electric field. Its capacity to store charge is known as capacitance, or how much charge needs to be distributed across the membrane for a certain potential to build up. An ideal capacitor has a constant capacitance, measured in farads (\(F\)), and is defined as the ratio between the positive/negative charge \(Q\) on the conductors and the voltage \(V\) across the dielectric: \[ C=QV \]

The relevant quantity for the membrane is the membrane capacitance \(C_m\), which is the capacitance per unit area of membrane. Capacitance affects how quickly the membrane potential changes (and the speed at which electrical signals propagate along the axon of the neuron). When the voltage across the capacitance changes, a current will flow.

The membrane capacitance of a cell is traditionally seen as a "biological constant" (Cole, 1969) at around \(\sim{1} \mu{F}/\text{cm}^{2}\), but in fact it has been estimated at various values in the literature (Gentet et al, 2000). A histogram of various values is plotted below:

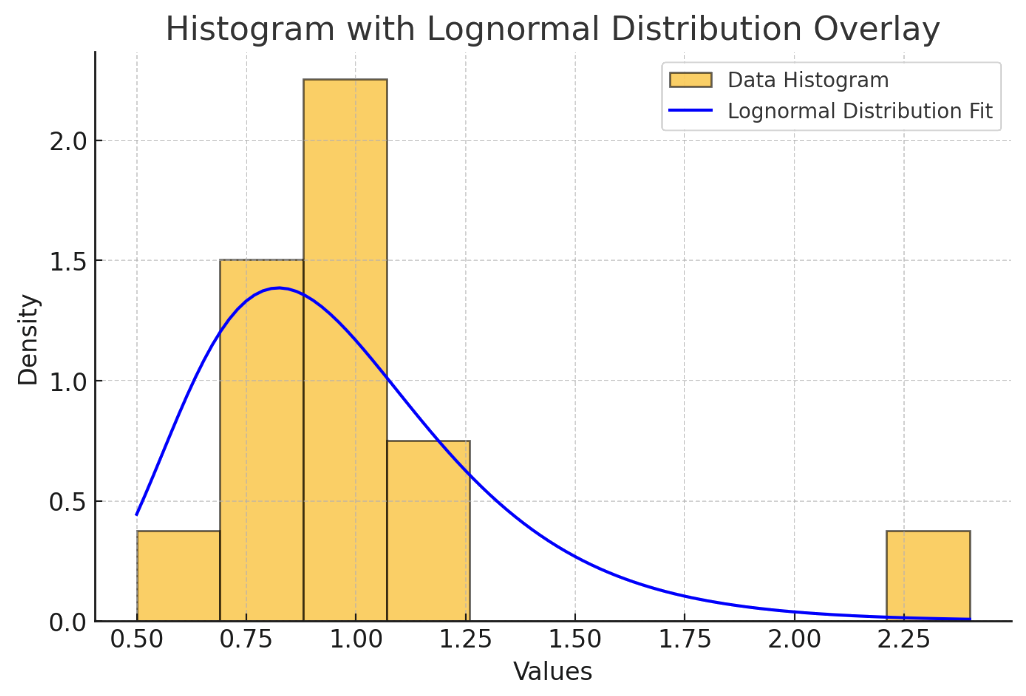Values of \(C_m\) from various studies

The mean value is \(0.98 \mu{F}/cm^2\). Combining this with the resting potential of \(−69mV\), this means a hypothetical spherical cell of radius \(5-\mu{m}\) would store \(−0.22×10^{−12}\) coloumbs of charge:

python

import math

def calculate_stored_charge(radius_micrometers, resting_potential_mV):
    radius_m = radius_micrometers * 1e-6  # meters
    V = resting_potential_mV * 1e-3  # volts
    C_m = 0.98e-2  # F/m²

    # Calculate the surface area (A) of the spherical cell
    A = 4 * math.pi * radius_m**2  # m²

    C = C_m * A
    Q = C * V

    return Q

radius_micrometers = 5  # µm
resting_potential_mV = -69  # mV

charge = calculate_stored_charge(radius_micrometers, resting_potential_mV)
print(charge)

-2.155132560362598e-13

The importance of capacitance for neural dynamics is its effect on the neuron's time constant, which is the time it takes for the membrane potential to respond to inputs (specifically, to reach 63% of its steady state value). This can be calculated as:

\[ \tau = R_mC_m \]

where \(R_{m}\) is the membrane resistance and \(C_{m}\) is the membrane capacitance. The larger the capacitance, the slower the change in the membrane potential.

The membrane resistance is the inverse of the membrane conductance, which is the sum of the conductances of all the ion channels in the membrane.

The high resistivity of the lipids prevents charge from passing across the membrane, so from an electrical perspective, the properties of membranes can be solely described by capacitance (Koch, 1999).

Notes on the Membrane

References